분산 (광학)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

분산(광학)은 매질 내에서 빛의 파장에 따라 속도가 달라지는 현상을 의미한다. 이는 빛의 파장이 달라짐에 따라 굴절률이 변하기 때문에 발생하며, 백색광이 프리즘을 통과할 때 여러 색깔로 분리되는 현상으로 쉽게 관찰할 수 있다. 분산은 빛의 파장과 굴절률 간의 관계를 나타내는 물질 분산과, 도파관 구조의 기하학적 특성에 의해 발생하는 도파관 분산으로 분류된다. 물질 분산은 분광기, 색수차 등 광학 응용 분야에 영향을 미치며, 도파관 분산은 광섬유 통신에서 펄스 확산을 일으켜 신호 전송 거리를 제한하는 요인으로 작용한다. 분산 제어는 광통신 시스템의 성능 향상과 레이저 펄스 제어에 중요한 역할을 하며, 정상 분산과 이상 분산으로 구분된다. 또한 펄서에서 방출되는 전파의 분산은 천문학 연구에 활용되며, 보석의 광채를 결정하는 중요한 요소로도 작용한다.

더 읽어볼만한 페이지

광학 - 광자
광자는 전자기파의 기본 입자이자 빛의 입자적 성질을 나타내는 양자이며, 전하를 띠지 않고 에너지와 운동량을 가지며 다양한 기술 분야에 응용된다.
광학 - 굴절
굴절은 빛이 한 매질에서 다른 매질로 진행할 때 속도 변화로 인해 진행 방향이 꺾이는 현상이며, 렌즈, 프리즘, 광섬유 등 다양한 분야에 응용된다.

분산 (광학)
구글 지도
분산 (광학)
개요
정의	빛의 파장에 따른 굴절률 변화 또는 빛의 파장에 따른 위상 속도 변화
설명	빛이 매질을 통과할 때 매질의 굴절률이 빛의 파장에 따라 달라져 빛이 분리되는 현상
원인	매질의 유전율이 빛의 주파수에 따라 다르기 때문에 발생
굴절률과 파장
관계	일반적으로 가시광선 영역에서 파장이 짧을수록 굴절률이 커짐
파장 변화	파장이 짧은 청색광은 파장이 긴 적색광보다 더 많이 굴절됨
결과	프리즘을 통과한 빛이 무지개 색으로 분리되는 현상
정상 분산과 이상 분산
정상 분산	굴절률이 파장이 증가함에 따라 감소하는 영역
이상 분산	굴절률이 파장이 증가함에 따라 증가하는 영역
발생	물질의 고유 흡수 주파수 근처에서 나타남
분산의 종류
물질 분산	매질의 굴절률이 빛의 파장에 따라 달라지는 현상
도파관 분산	도파관의 구조적 특성에 의해 발생하는 분산
편광 모드 분산	광섬유에서 편광 방향에 따른 속도 차이로 발생하는 분산
모드 분산	광섬유에서 여러 모드가 존재하여 속도 차이가 나는 현상
응용
분광기	빛을 파장별로 분리하여 분석하는 기기
프리즘	빛을 분산시켜 스펙트럼을 만드는 데 사용
광섬유 통신	광섬유 내에서 빛의 분산은 신호 품질에 영향을 미치므로 보상 기술이 사용됨
렌즈 설계	색수차를 보정하는 데 분산 특성이 고려됨
색수차	분산으로 인해 렌즈가 초점을 정확하게 맞추지 못하는 현상
수학적 표현
굴절률	복소수 굴절률을 사용하여 표현 가능
코시의 공식	매질의 굴절률을 파장의 함수로 나타내는 근사식
셀마이어 방정식	매질의 굴절률을 파장의 함수로 더 정확하게 나타내는 식
군속도 분산 (GVD)	파장 변화에 따른 군속도의 변화율을 나타내는 값
군속도 분산 (GVD)	β2 또는 D로 표시
군속도 분산 (GVD)	광섬유의 분산 계수를 나타내는 데 사용
군속도 분산 (GVD)	단위는 ps/nm/km

2. 이론

매질 속에서 빛의 파장과 굴절률의 관계, 전자기파의 속력, 군속도, 유전율, 투자율 등 분산 현상을 설명하는 다양한 이론적 배경을 제시한다.

고전물리학에서 빛은 모든 파장의 전자기파로 정의되며, 맥스웰 방정식에 따라 매질의 유전율과 투자율에 의해 전자기파의 속력이 결정된다. 굴절률은 이러한 유전율과 투자율의 비율로 표현할 수 있다.^[3]

매질이 선형이고 고르다면, 유전율(ε)과 투자율(μ)은 변하지 않고 상수로 취급할 수 있다. 이때 전자기파의 속력은 $v=\frac{1}{\sqrt{\varepsilon\mu}}$ 이다. 투명한 매질 속에서 빛의 속력은 굴절률 n의 역수만큼 감소하여 $v=\frac{c}{n}$ 이 되고, $c=\frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}$ 이므로, 굴절률 n은 $n=\sqrt{\frac{\varepsilon\mu} {\varepsilon_{0}\mu_{0}}}$ 으로 나타낼 수 있다.

하지만 실제로 유전율(ε), 투자율(μ), 전도도(σ)는 전자기파의 진동수에 따라 변한다. 진동수가 다른 파동은 매질에 따라 속도가 달라지며, 여러 진동수가 섞인 파동은 매질 속을 지나면서 모양이 변한다. 전자기파는 이동하며 에너지를 전달하고, 에너지 전달 속도는 군속도 $v_{g}=\frac{dw}{dk}$ 로 나타낸다.

물질의 유전율(ε), 투자율(μ), 전도도(σ)는 진동수(w)의 함수로 표현되지만, 투자율(μ)은 대부분의 물질에서 투자율(μ0)와 큰 차이가 없어 w에 대한 변화가 거의 없다. 따라서 유전율과 전도도를 고려해야 하며, 분자 수준 근사를 통해 ε(w)와 μ(w)를 알 수 있다.

절연체 매질에서 전자는 결합력 때문에 분자에 붙어 있으며, 상수 k인 용수철 끝에 달린 것으로 생각할 수 있다. 변위 y, 전자 질량 m, 고유진동수 $\omega_{0}=\sqrt{\frac{k}{m}}$ 일 때, $F=-ky=-m\omega_{0}^{2}y$ 이며, $\varepsilon=\varepsilon_{0}[1+\frac{Nq^{2}}{m\varepsilon_{0}}\sum\frac{f_{j}}{(\omega_{j}^{2}-\omega^{2})-i\gamma_{j}\omega}]$ , $k=\sqrt{\varepsilon\mu_{0}}\omega$ 이다.

일반적으로 ε의 두 번째 항이 작으므로, $k\cong\frac{\omega}{c}[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}}{(\omega_{j}^{2}-\omega^{2})-i\gamma_{j}\omega}]$ 로 근사할 수 있다. 따라서 굴절률은 다음과 같이 나타낼 수 있다.

: $n\cong[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}(\omega_{j}^{2}-\omega^{2})}{(\omega_{j}^{2}-\omega^{2})^{2}+\gamma_{j}\omega}]$

선형 응답 이론에서 주파수 응답 함수의 실수부 변화를 '''분산''', 허수부 변화를 '''흡수'''라고 하며, 크라머스-크로니히 관계식이 성립한다. 주파수 응답 함수의 유형에 따라 '''완화형'''과 '''공명형'''으로 나눌 수 있다.

2. 1. 굴절률과 파장의 관계

매질 속에서의 파장은

\lambda = \lambda_0 /n

으로, 진공에서의 파장(

\lambda_0

)을 굴절률(n)로 나눈 값이다. 일반적으로 파장이 증가하면 굴절률은 감소한다.^[3] 따라서 백색광이 프리즘을 통과할 때 파장이 큰 빛인 붉은빛이 가장 적게 꺾이고, 보라빛이 가장 크게 꺾이게 된다.

고전물리학에서는 빛을 모든 파장의 전자기파로 정의한다. 투명한 매질 속에서 빛의 속력은 굴절률 n의 역수만큼 감소하므로

v=\frac{c}{n}

이 된다.

크라머스-크로니히 관계 때문에 굴절률 실수부의 파장 의존성은 굴절률 허수부(소광 계수라고도 함)로 설명되는 물질 흡수와 관련이 있다.

광학에서 분산의 가장 일반적으로 관찰되는 결과는 프리즘에 의해 백색광이 색 스펙트럼으로 분리되는 것이다. 스넬의 법칙에서 프리즘에서 빛의 굴절 각도는 프리즘 재료의 굴절률에 따라 달라지는 것을 알 수 있다. 굴절률이 파장에 따라 변하므로, 빛이 굴절되는 각도도 파장에 따라 변하여 ''각 분산''으로 알려진 색상의 각 분리가 발생한다.

가시광선의 경우, 대부분의 투명 물질(예: 공기, 유리)의 굴절률 ''n''은 파장 ''λ''이 증가함에 따라 감소한다.

:

1 < n(\lambda_\text{red}) < n(\lambda_\text{yellow}) < n(\lambda_\text{blue}),

또는 일반적으로,

:

\frac{dn}{d \lambda} < 0.

이 경우 매질은 ''정상 분산''을 갖는다고 한다. 반대로 지수가 파장이 증가함에 따라 증가하는 경우(일반적으로 자외선에서의 경우^[4]), 매질은 ''비정상 분산''을 갖는다고 한다.

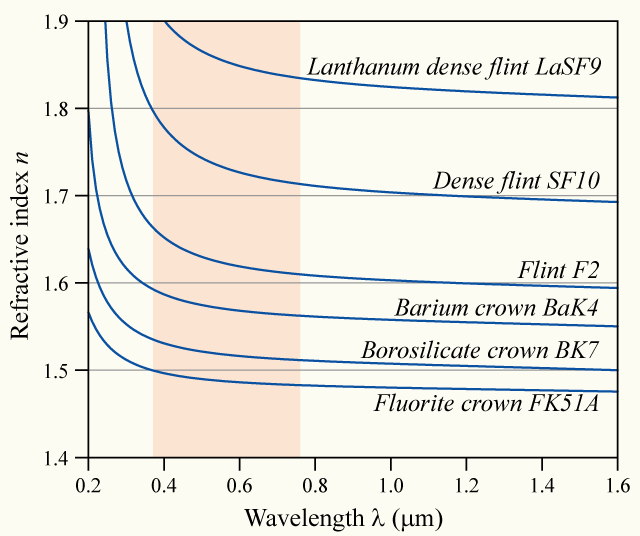
다양한 유리에서 굴절률과 진공 파장의 관계(정상 분산). 얇은 빨간색으로 칠해진 부분은 가시광선 영역.

파장이 짧아질수록 굴절률이 증가하는 경우를 '''정상 분산'''(normal dispersion^영어)이라고 한다. 가시광선 영역에서 투명한 물질은 가시광선 영역에서 정상 분산이 일어난다. 가시광선 이외에도 물질의 공명 파장에서 벗어난 영역에서는 정상 분산이 일어난다. 또한 일반적으로 굴절률이 높은 물질일수록 정상 분산이 더 크다.

이와 반대로, 공명 파장 부근에서는 굴절률이 감소하고, 장파장광이 단파장광보다 크게 굴절한다. 이것을 '''이상 분산'''(anomalous dispersion^영어)이라고 한다.

일반적으로 굴절률은 다음 식과 같이 나타낼 수 있다.

:

n\cong[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}(\omega_{j}^{2}-\omega^{2})}{(\omega_{j}^{2}-\omega^{2})^{2}+\gamma_{j}\omega}]

위 식에서 진동수가 공명진동수 근처가 되면 굴절률이 감소하는데 이를 비정상 분산이라고 하며, 일반적으로 잘 일어나지 않는다. 그리고 진동수가 공명진동수와 유사할때를 제외한다면, 진동수가 커질 때 굴절률이 증가한다는 것을 식을 통해서 확인할 수 있다.

공명 파장 및 그 근방 이외의 굴절률은 셀마이어의 분산 공식으로 나타낼 수 있다.

:

n^2 = n_\infty^2 + {A' \over \lambda^2 - {\lambda_A}^2} + {B' \over \lambda^2 - {\lambda_B}^2} + \dots

'''A′''', '''B′''', ... 및 '''λ''', '''λ''', ...는 물질에 따라 다른 매개변수이다. '''λ''', '''λ''', ...는 공명 파장이며, ('''n''' 이외의) 항은 공명 파장의 수만큼 존재한다.

이것을

\lambda

에 대해 급수 전개하면 다음 식이 된다.

:

n^2 = A + {B\over \lambda^2} + {C\over \lambda^4} + \cdots - B' \lambda^2 - C' \lambda^4 - \cdots

셀마이어의 분산 공식은 공명 파장에서는 발산한다. 그러나 그 근방 이외에서는 정상 분산과 이상 분산에 대해 좋은 일치를 보인다.

밀도가 높은 매질에서는 적외선 영역에 있는 이온 공명 파장을 고려한 셀마이어의 분산 공식이 사용된다. 일반적으로 투명한 매질은 절연체(유전체)이다. 이때 매질 속 분자가 전자파의 전기장에 의해 분극되는 전기쌍극자 모델로 근사할 수 있지만, 공명파장이 자외선 영역에 있으므로 기체와 같은 밀도가 낮은 매질(굴절률

n \approx 1

)에서는 가시광선 영역에서 다음 식으로 근사할 수 있는 것으로 알려져 있다(오귀스탱 루이 코시에 의해 경험적으로 구해졌으므로 코시의 분산 공식이라고 한다). 다음에서 A, B, C 등은 측정에 의해 결정되는 상수이다.

:

n - 1 = A \left( 1 + {B \over \lambda^2}\right)

코시의 분산 공식은 셀마이어의 분산 공식의 근사 형태이다.

2. 2. 전자기파와 굴절률

고전물리학에서 빛은 모든 파장의 전자기파로 정의되며, 맥스웰 방정식에 따라 매질의 유전율과 투자율에 의해 전자기파의 속력이 결정된다. 굴절률은 이러한 유전율과 투자율의 비율로 표현할 수 있다.^[3]

맥스웰 방정식에서 매질이 선형이고 고르다면 유전율 (ε) 와 투자율 (μ)가 변하지 않으므로 상수로 취급할 수 있다. 이때 전자기파의 속력은

v=\frac{1}{\sqrt{\varepsilon\mu}}

가 된다. 투명한 매질 속에서 빛의 속력은 굴절률 n의 역수만큼 감소하므로

v=\frac{c}{n}

이 되고,

c=\frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}

이므로, 굴절률 n은

n=\sqrt{\frac{\varepsilon\mu} {\varepsilon_{0}\mu_{0}}}

과 같이 표시할 수 있다.

이 과정에서 유전율ε, 투자율μ, 전도도σ를 상수로 취급하였지만, 실제로 이 매개변수들은 전자기파의 진동수에 따라 어느 정도 변하게 된다. 진동수가 다른 파는 매질에 따라 움직이는 속도가 달라진다. 따라서 여러 가지 진동수가 섞여있는 파는 매질 속을 진행하면서 파의 모양이 바뀌게 된다. 이때 전자기파는 이동하면서 에너지를 전달하게 되고, 에너지의 전달 속도는 군속도

v_{g}=\frac{dw}{dk}

로 표현된다. 전자기장에 대한 물질의 반응인 유전율ε, 투자율μ, 전도도σ는 진동수w의 함수로 표현 될 것이지만, 투자율μ은 많은 물질에서 투자율μ0와 큰 차이가 없으므로 w 에 대한 변화는 거의 없다. 그러므로 유전율과 전도도를 고려해야 하며, 분자 수준에서의 근사를 통해 ε(w)와 μ(w)를 알아 낼 수 있다.

매질이 절연체일 때 전자는 결합력 때문에 분자에 붙어 있으므로, 전자가 상수 k인 용수철 끝에 달린 것이라고 생각한다면 변위 y, 전자 질량 m, 고유진동수

\omega_{0}=\sqrt{\frac{k}{m}}

이라고 할 때,

F=-ky=-m\omega_{0}^{2}y

되며 이 때,

\varepsilon=\varepsilon_{0}[1+\frac{Nq^{2}}{m\varepsilon_{0}}\sum\frac{f_{j}}{(\omega_{j}^{2}-\omega^{2})-i\gamma_{j}\omega}]

,

k=\sqrt{\varepsilon\mu_{0}}\omega

이다.

일반적으로 ε의 두 번째 항이 작으므로

k\cong\frac{\omega}{c}[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}}{(\omega_{j}^{2}-\omega^{2})-i\gamma_{j}\omega}]

처럼 근사할 수 있다. 따라서 굴절률은

n\cong[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}(\omega_{j}^{2}-\omega^{2})}{(\omega_{j}^{2}-\omega^{2})^{2}+\gamma_{j}\omega}]

와 같다.

위 식에서 진동수가 공명진동수 근처가 되면 굴절률이 감소하는데 이를 비정상 분산이라고 하며, 일반적으로 잘 일어나지 않는다. 그리고 진동수가 공명진동수와 유사할 때를 제외한다면, 진동수가 커질 때 굴절률이 증가한다는 것을 식을 통해서 확인할 수 있다.^[4]

2. 3. 군속도와 분산

전자기파의 에너지는 군속도로 전달되며, 군속도는 진동수에 따라 달라진다. 이러한 군속도의 변화가 분산 현상의 핵심 원인 중 하나이다.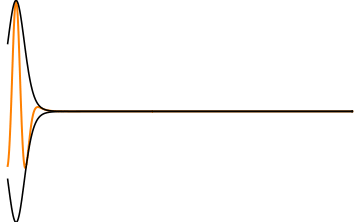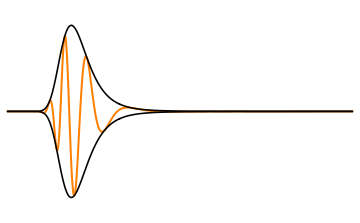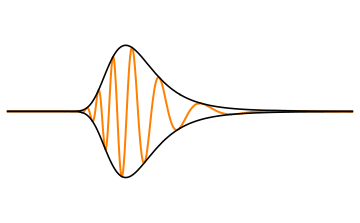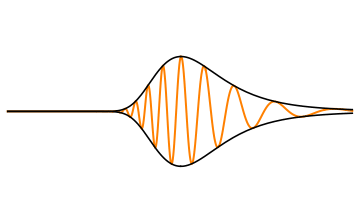

파장에 따른 위상 속도의 변화를 단순히 설명하는 것을 넘어, 많은 응용 분야에서 분산의 더 심각한 결과는 군속도 분산(Group-velocity dispersion, GVD)이다. 위상 속도 ''v''는 ''v'' = ''c''/''n''으로 정의되지만, 이것은 하나의 주파수 성분만을 설명한다. 신호나 펄스를 고려할 때처럼 서로 다른 주파수 성분이 결합될 때는, 파에 중첩된 펄스나 정보(변조)가 전파되는 속도를 나타내는 군속도(group velocity)에 더 관심을 갖는 경우가 많다. 첨부된 애니메이션에서 볼 수 있듯이, 파 자체(주황색-갈색)는 군속도에 해당하는 ''봉투''(검정색)의 속도보다 훨씬 빠른 위상 속도로 이동한다. 이 펄스는 예를 들어 통신 신호일 수 있으며, 더 빠른 속도(위상 속도)로 진행하는 파면으로 구성되어 있더라도, 그 정보는 군속도로만 전파된다.

굴절률 곡선 ''n''(''ω'') 또는 파수 ''k'' = ''ωn''/''c''로부터 군속도를 계산할 수 있다. 여기서 ''ω''는 각 주파수 ''ω'' = 2''πf''이다. 위상 속도에 대한 한 가지 표현식은 ''v''_p = ''ω''/''k''이지만, 군속도는 미분을 사용하여 ''v''_g = ''dω''/''dk''로 표현할 수 있다. 또는 위상 속도 ''v''_p의 관점에서 다음과 같이 표현할 수 있다.

:

v_\text{g} = \frac{v_\text{p}}{1 - \dfrac{\omega}{v_\text{p}} \dfrac{dv_\text{p}}{d\omega}}.

분산이 존재하면 군속도가 위상 속도와 같지 않을 뿐만 아니라, 일반적으로 군속도 자체가 파장에 따라 달라진다. 이것을 군속도 분산이라고 하며, 펄스 내의 서로 다른 주파수 성분이 다른 속도로 이동하기 때문에 짧은 광 펄스가 확장되는 원인이 된다. 군속도 분산은 군속도의 역수에 대한 각 주파수에 대한 미분으로 정량화되며, 군속도 분산 = ''d''²''k''/''dω''²로 나타낼 수 있다.

광 펄스가 양의 군속도 분산을 가진 물질을 통해 전파되면, 단파장 성분이 장파장 성분보다 느리게 이동한다. 따라서 펄스는 시간에 따라 주파수가 증가하는 ''양의 쳐핑''(up-chirped)이 된다. 반면에 펄스가 음의 군속도 분산을 가진 물질을 통해 전파되면, 단파장 성분이 장파장 성분보다 빠르게 이동하고 펄스는 시간에 따라 주파수가 감소하는 ''음의 쳐핑''(down-chirped)이 된다.

음향 영역에서 음의 쳐핑 신호의 일상적인 예로는 용접된 선로의 변형에 부딪히는 다가오는 기차의 소리가 있다. 기차 자체가 발생시키는 소리는 충격적이며 금속 선로에서 공기보다 훨씬 빠르게 이동하므로 기차가 도착하기 훨씬 전에 들을 수 있다. 그러나 멀리서 들리는 소리는 충격을 일으키는 것으로 들리지 않고, 선로의 진동 모드 복잡성에 의한 잔향 속에서 독특한 내려가는 쳐핑 소리를 낸다. 군속도 분산은 소리의 크기가 수 초에 달하는 놀라울 정도로 오랫동안 들리는 것으로 들을 수 있다.

2. 4. 비정상 분산

위 식에서 진동수가 공명진동수 근처가 되면 굴절률이 감소하는데, 이를 비정상 분산이라고 하며 일반적으로 잘 일어나지 않는다. 진동수가 공명진동수와 유사할 때를 제외하면 진동수가 커질 때 굴절률이 증가한다는 것을 식을 통해 확인할 수 있다. 공명 파장 부근에서는 굴절률이 감소하고, 장파장광이 단파장광보다 크게 굴절하는데, 이것을 '''이상 분산'''(anomalous dispersion^영어)이라고 한다.

3. 뉴턴의 색이론

뉴턴은 1665년 페스트 유행으로 케임브리지 대학교가 2년간 폐교되자, 집에서 프리즘을 이용한 여러 실험을 하였다. 당시 프리즘은 무지개를 만드는 장난감과 비슷하게 여겨졌는데, 뉴턴은 백색광을 프리즘에 통과시켰을 때 나타나는 무지개색을 관찰하면서 백색광을 이루는 여러 색의 빛이 프리즘에서 서로 다르게 굴절된다고 생각하였다.^[1]

뉴턴은 이 가설을 증명하기 위해, 작은 구멍으로 들어온 빛을 프리즘으로 분리시킨 후 분리된 각 색깔의 빛을 다시 프리즘에 통과시키는 실험을 하였다. 그 결과, 2차 분산이 발생하지 않는다는 것을 확인하여 백색광이 여러 색깔의 빛이 혼합되어 있다는 것을 증명하였다.^[1]

3. 1. 아리스토텔레스와 데카르트의 설

17세기까지는 색이 흰색과 검은색, 밝음과 어두움의 혼합에 의해 생긴다는 아리스토텔레스의 설이 그대로 통용되었으나 이는 가짜 아리스토텔레스의 문서에서 유래한 것이다.^[1] 데 도미니스는 1611년에 출판한 광학서에서 빛을 차단하거나 또는 없애서 빛에 어두움을 섞으면 색이 생긴다고 서술하였다.^[1]

데카르트는 우주공간이 미세한 물질로 채워져 있다고 주장하였다.^[1] 이 물질은 전체적으로 또는 물질 하나하나에 회전운동을 하고 있는데, 이때 전체적인 회전운동은 행성운동의 원인이고, 물질 하나하나의 운동은 색의 차이를 일으킨다고 하였다.^[1] 데카르트는 광선을 우주공간에 채워진 물질의 압력이라고 설명하며, 우리의 눈은 이 압력을 빛으로 인지하고, 물질 하나하나의 운동을 색으로 느낀다고 하였다.^[1] 이러한 회전운동은 밀도가 큰 매질의 영향을 받아서 변화를 일으키게 되며 이것이 스펙트럼의 원인이 된다. 이때 적색은 강한 회전이며, 자주색은 약한 회전운동이고, 프리즘은 이러한 회전운동에 영향을 주는 것이라고 설명하였다.^[1]

이러한 이론은 당시 사람들에게 잘 받아들여지지는 않았지만, 빛과 색을 기계적으로 설명하려고 하였다는 점에서 의의가 있다.^[1]

3. 2. 뉴턴의 프리즘 실험

1665년 케임브리지 대학교 학생이었던 뉴턴은 페스트 유행으로 학교가 2년간 폐교되자, 집에서 프리즘을 이용한 여러 실험을 하였다. 당시 프리즘은 무지개를 만드는 장난감과 비슷하게 여겨졌는데, 뉴턴은 백색광을 프리즘에 통과시켰을 때 나타나는 무지개색을 관찰하면서 백색광을 이루는 여러 색의 빛이 프리즘에서 서로 다르게 굴절된다고 생각하였다.^[1]

뉴턴은 이러한 생각을 증명하기 위해, 작은 구멍으로 들어온 빛을 프리즘으로 분리시킨 후 분리된 각 색깔의 빛을 다시 프리즘에 통과시키는 실험을 하였다. 그 결과, 2차 분산이 발생하지 않는다는 사실을 확인하여 백색광이 여러 색깔의 빛이 혼합되어 있다는 것을 증명하였다.^[1]

4. 분산 현상

분산은 빛이 파장에 따라 굴절되는 정도가 다른 현상이다. 무지개는 분산의 가장 친숙한 예시로, 흰색 빛이 서로 다른 파장(색깔)으로 분리되는 현상을 보여준다. 분산은 광섬유에서 펄스가 퍼져 장거리 신호를 저하시키는 군속도 분산 현상이나, 군속도 분산과 비선형 효과의 상쇄로 발생하는 솔리톤파 등 다양한 현상에 영향을 미친다.

사진 및 현미경 렌즈에서 분산은 색수차를 일으켜 이미지의 색상이 제대로 겹쳐지지 않게 한다. 이를 막기 위해 아크로매트와 같이 서로 다른 분산 특성을 가진 유리를 사용하는 다중 요소 렌즈 등 여러 기술이 개발되었다.^[1]

4. 1. 프리즘

프리즘은 빛을 파장별로 분리하여 분산을 관찰하는 데 사용되는 대표적인 광학 기기이다. 백색광은 여러 가지 파장을 가지는 빛의 혼합으로 이루어져 있는데, 프리즘에 백색광을 입사시키면 파장별로 굴절률이 달라 굴절각이 달라지는 현상이 발생한다. 이때문에 파장이 긴 빨간색 빛부터 파장이 짧은 보라색 빛까지 분리되어 나타난다. 스넬의 법칙에 따르면, 프리즘에서 빛의 굴절 각도는 프리즘 재료의 굴절률에 따라 달라진다. 굴절률은 파장에 따라 변하므로, 빛이 굴절되는 각도도 파장에 따라 변하여 색상의 각 분리가 발생하며, 이를 ''각 분산''이라고 한다.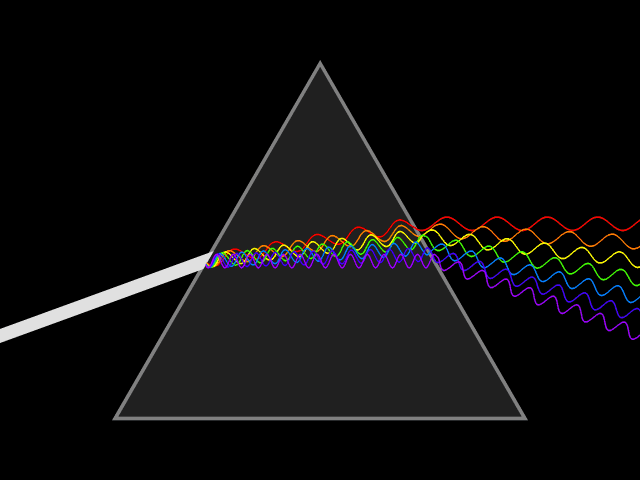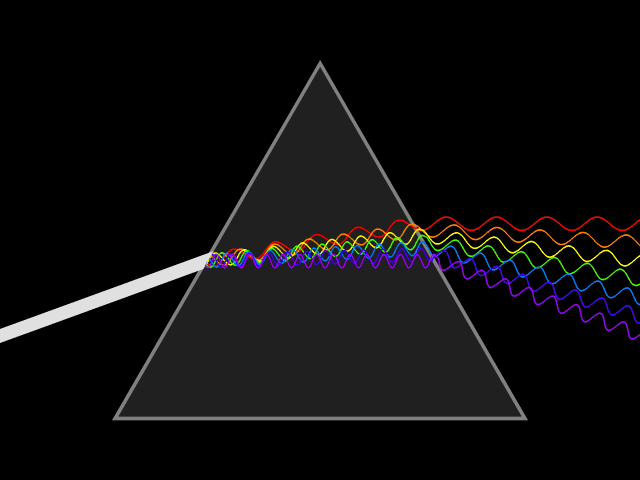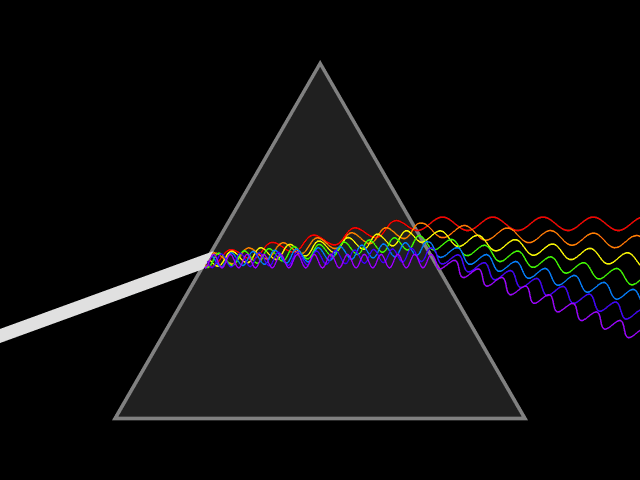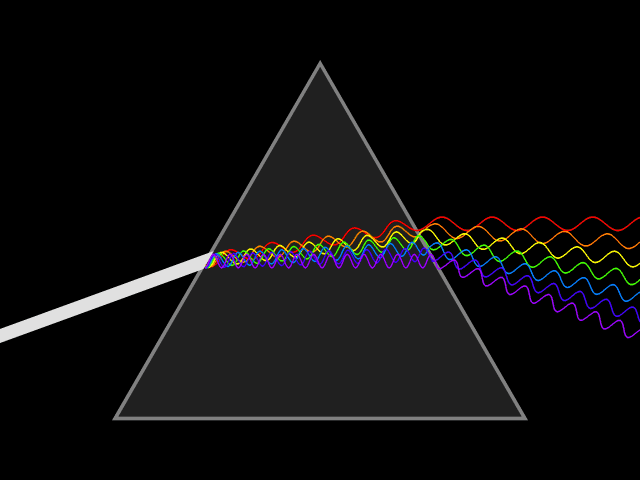

가시광선의 경우, 대부분의 투명 물질(예: 공기, 유리)의 굴절률 ''n''은 파장 ''λ''이 증가함에 따라 감소한다.

:

1 < n(\lambda_\text{red}) < n(\lambda_\text{yellow}) < n(\lambda_\text{blue})

일반적으로 다음과 같이 표현할 수 있다.

:

\frac{dn}{d \lambda} < 0.

이러한 경우 매질은 ''정상 분산''을 갖는다고 한다. 반대로 굴절률이 파장이 증가함에 따라 증가하는 경우는 ''비정상 분산''을 갖는다고 한다.

공기와 같은 물질의 경계면에서, 스넬의 법칙은 법선에 대해 ''θ'' 각도로 입사하는 빛이

\arcsin\left(\frac{\sin\theta}{n}\right)

각도로 굴절될 것이라고 예측한다. 따라서 굴절률이 높은 청색광은 적색광보다 더 강하게 굴절되어 무지개와 같은 패턴을 생성한다.

4. 2. 무지개

무지개는 일상 생활에서 쉽게 접할 수 있는 분산의 대표적인 현상이다. 비가 온 후에 대기 중에 떠다니는 작은 물방울들이 프리즘 역할을 하여 태양빛을 분산시킨다. 이 물방울들에 태양빛이 입사한 후 굴절되는 과정에서 분산이 일어난다.^[1]

보라색 빛은 빨간색 빛에 비해 굴절률이 크므로 같은 입사각으로 입사했을 때 더 큰 굴절각을 가지며 물방울 속으로 입사한다. 이렇게 입사한 빛은 물방울 속에서 한번 반사된 후 물방울과 공기의 경계에서 다시 굴절되어 눈으로 들어오게 된다. 따라서 태양을 등지고 있어야 무지개를 관찰할 수 있다.^[1]

태양광은 평행하게 지구에 입사하지만 물방울의 표면은 곡면이므로 결과적으로 태양광은 물방울에 대해 다양한 입사각을 가진다. 따라서 서로 다른 각도로 굴절과 반사를 하게 되고 여러 가지 각도로 물방울을 빠져나온다. 이렇게 진행하는 빛을 추적해 보면 빛이 여러 각도에서 균일하게 퍼지는 것이 아니라, 입사광선에 대해 최소편위각의 방향으로 많은 빛이 나온다. 그러므로 물방울에 평행하게 입사한 빛은 균일하게 퍼지지 않고, 특정한 각도로 많은 양의 빛이 퍼져나가게 되는데 이때의 특정 각도를 무지개각이라고 한다. 무지개각은 빨간색 빛의 경우 42˚이고 보라색 빛은 41˚이다.^[1]

대기 중에 떠다니는 물방울이 수없이 많이 존재하므로, 우리가 물방울을 바라보았을 때 42도의 각도를 가지는 물방울에서는 빨간색 빛이 우리 눈에 입사하고, 41도의 각도를 가지는 물방울에서는 보라색 빛이 우리 눈에 입사한다. 42˚ 이상이나 41˚ 이하의 물방울에서 나오는 빛은 우리 눈에 들어오지 않게 되며, 따라서 무지개는 빨간색 빛이 바깥쪽에 위치하고, 보라색 빛이 안쪽에 위치하게 된다. 또한 빨간색 빛은 42˚의 물방울에서 굴절 및 반사되어 오는 빛이고, 보라색 빛은 41˚에서 반사되어 오는 빛이므로, 우리가 무지개를 향해 이동하여도 무지개에 가까워질 수 없으며, 해당하는 각도에 있는 다른 물방울에 의해 굴절 및 반사되어 오는 빛에 의한 무지개를 관찰할 수밖에 없다.^[1]

4. 3. 쌍무지개

뚜렷하고 선명한 일차 무지개 주위로 희미한 이차 무지개가 나타나는 것을 쌍무지개라 한다. 이차무지개는 일차 무지개에 비해 색이 흐리고 색의 배열이 반대이다. 이러한 이차 무지개는 물방울에 입사한 백색광이 물방울 내에서 두 번 반사하여 만들어진다. 이때 두 번의 반사를 거치므로 공기중으로 굴절되어 나가는 빛의 양이 일차무지개에 비해 많게 되고, 따라서 이차 무지개는 일차무지개에 비해 희미하게 보이게 된다.

보라색 빛은 빨간색빛보다 굴절률이 크므로 더 큰 각도로 물방울 안으로 굴절하고, 두 번의 내부 반사를 거친 후 물방울을 빠져 나올 때는 일차 무지개와 비교했을 때 반대의 색 배치를 갖게 된다. 이때 무지개각은 빨간색 빛이 50˚, 보라색빛은 54˚이다. 따라서 일차 무지개에 비해 더 큰 각을 갖게 되므로 크기가 더 커 보이며, 색의 배열이 반대가 된다.

4. 4. 달무리

달무리는 엷은 구름이 끼어있을 때 달 주위에 나타나는 동그란 띠를 말한다. 달무리는 대기 중에 떠 있는 얼음 결정에 의해서 빛이 두 번 굴절되기 때문에 발생한다. 결정에 입사된 빛이 결정면에서 한번 굴절되고, 결정을 나가면서 또한번 굴절하는데, 이때 22도의 굴절각을 가지게 된다. 따라서 달무리는 달을 중심으로 22도의 원형으로 관찰된다.

달무리가 넓을 때는 색이 희게 보이나, 달무리가 짙을 때는 안쪽은 붉은색, 바깥쪽은 노란색을 띤다.

5. 물질 분산과 도파관 분산

광섬유는 현대 통신 시스템에서 널리 사용되는 빛에 대한 일종의 도파관이다. 광섬유에서는 물질 분산과 도파관 분산이 나타나는데, 이 두 분산은 서로 상쇄되어 영분산 파장을 생성할 수 있으며, 이는 고속 광섬유 통신에 중요하다.^[5]

물질 분산: 주로 물질의 굴절률이 빛의 주파수에 따라 변화하는 현상이다.
도파관 분산: 도파관에서 파동의 위상 속도가 구조의 기하학적 형상 때문에 주파수에 따라 달라지는 현상이다.

일반적으로 전파 상수 β에서 각진동수 ω(β)를 갖는 도파관 모드의 경우 (전파 방향 z에서 전자기장이 e^i(βz−ωt)에 비례하여 진동함), 군 속도 분산 매개변수 D는 다음과 같이 정의된다.^[5]

:

D = -\frac{2\pi c}{\lambda^2} \frac{d^2 \beta}{d\omega^2} = \frac{2\pi c}{v_g^2 \lambda^2} \frac{dv_g}{d\omega},

여기서 λ = 2πc/ω는 진공 파장이고, v_g = dω/dβ는 군 속도이다. 이 공식은 도파관 분산과 재료 분산을 모두 포함한다. |D|는 단위 거리당 단위 대역폭 Δλ당 시간 펄스 확산 Δt를 나타내며, 광섬유의 경우 일반적으로 ps/(nm⋅km) 단위로 보고된다.

다모드 광섬유의 경우, 모드 분산도 펄스 확산을 일으킨다. 단일 모드 광섬유에서도 편광 모드 분산으로 인해 펄스 확산이 발생할 수 있는데, 이는 색 분산의 예가 아니다.

5. 1. 물질 분산

색 분산은 주로 물질의 굴절률이 광학 주파수에 따라 변화하는 현상이다. 대부분의 경우, 색 분산은 벌크 재료 분산, 즉 광학 주파수에 따른 굴절률의 변화를 의미한다.^[3]

물질 분산은 광학 응용 분야에서 바람직하거나 바람직하지 않은 효과가 될 수 있다. 유리 프리즘에 의한 빛의 분산은 분광기와 분광복사계를 만드는 데 사용된다. 그러나 렌즈에서 분산은 색수차를 발생시키는데, 이는 현미경, 망원경 및 사진 렌즈의 이미지를 저하시키는 바람직하지 않은 효과이다.

주어진 균일 매질에서 파동의 위상 속도 ''v''는 다음과 같이 주어진다.

:

v = \frac{c}{n},

여기서 ''c''는 진공에서의 빛의 속도이고, ''n''은 매질의 굴절률이다.

일반적으로 굴절률은 빛의 주파수 ''f''의 함수이므로, ''n'' = ''n''(''f'') 또는 파장에 대해 ''n'' = ''n''(''λ'')로 표현할 수 있다. 물질의 굴절률의 파장 의존성은 일반적으로 아베 수 또는 코시 또는 셀마이어 방정식과 같은 경험적 공식의 계수로 정량화된다.

크라머스-크로니히 관계 때문에 굴절률 실수부의 파장 의존성은 굴절률 허수부(소광 계수라고도 함)로 설명되는 물질 흡수와 관련이 있다.

다양한 유리의 굴절률 대 진공 파장 변화. 가시광선의 파장은 회색으로 음영 처리됨.

광학에서 분산의 가장 일반적으로 관찰되는 결과는 프리즘에 의해 백색광이 색 스펙트럼으로 분리되는 것이다. 스넬의 법칙에서 프리즘에서 빛의 굴절 각도는 프리즘 재료의 굴절률에 따라 달라지는 것을 알 수 있다. 굴절률이 파장에 따라 변하므로, 빛이 굴절되는 각도도 파장에 따라 변하여 ''각 분산''으로 알려진 색상의 각 분리가 발생한다.

가시광선의 경우, 대부분의 투명 물질(예: 공기, 유리)의 굴절률 ''n''은 파장 ''λ''이 증가함에 따라 감소한다.

:

1 < n(\lambda_\text{red}) < n(\lambda_\text{yellow}) < n(\lambda_\text{blue}),

또는 일반적으로,

:

\frac{dn}{d \lambda} < 0.

이 경우 매질은 ''정상 분산''을 갖는다고 한다. 반대로 지수가 파장이 증가함에 따라 증가하는 경우(일반적으로 자외선에서의 경우^[4]), 매질은 ''비정상 분산''을 갖는다고 한다.

공기 또는 진공(약 1의 지수)과 같은 물질의 경계면에서 스넬의 법칙은 법선에 대해 ''θ'' 각도로 입사하는 빛이 arcsin() 각도로 굴절될 것이라고 예측한다. 따라서 더 높은 굴절률을 갖는 청색광은 적색광보다 더 강하게 굴절되어 잘 알려진 무지개 패턴을 생성한다.

파장이 짧아질수록 굴절률이 증가하는 경우를 '''정상 분산'''(normal dispersion^영어)이라고 한다. 가시광선 영역에서 투명한 물질은 정상 분산이 일어난다. 가시광선 이외에도 물질의 공명 파장에서 벗어난 영역에서는 정상 분산이 일어난다. 또한 일반적으로 굴절률이 높은 물질일수록 정상 분산이 더 크다.

이와 반대로, 공명 파장 부근에서는 굴절률이 감소하고, 장파장광이 단파장광보다 크게 굴절한다. 이것을 '''이상 분산'''(anomalous dispersion^영어)이라고 한다. 공명 파장 및 그 근방 이외의 굴절률은 셀마이어의 분산 공식으로 나타낼 수 있다.

:

n^2 = n_\infty^2 + {A' \over \lambda^2 - {\lambda_A}^2} + {B' \over \lambda^2 - {\lambda_B}^2} + \dots

'''A′''', '''B′''', ... 및 '''λ''', '''λ''', ...는 물질에 따라 다른 매개변수이다. '''λ''', '''λ''', ...는 공명 파장이며, ('''n''' 이외의) 항은 공명 파장의 수만큼 존재한다.

이것을

\lambda

에 대해 급수 전개하면 다음 식이 된다.

:

n^2 = A + {B\over \lambda^2} + {C\over \lambda^4} + \cdots - B' \lambda^2 - C' \lambda^4 - \cdots

일반적으로 투명한 매질은 절연체(유전체)이다(도체라면 에너지가 줄열로 흡수된다). 이때 매질 속 분자가 전자파의 전기장에 의해 분극되는 전기쌍극자 모델로 근사할 수 있지만, 공명파장이 자외선 영역에 있으므로 기체와 같은 밀도가 낮은 매질(굴절률

n \approx 1

)에서는 가시광선 영역에서 다음 식으로 근사할 수 있다(오귀스탱 루이 코시(Augustin-Louis Cauchy)에 의해 경험적으로 구해졌으므로 코시의 분산 공식이라고 한다). 다음에서 A, B, C 등은 측정에 의해 결정되는 상수이다.

:

n - 1 = A \left( 1 + {B \over \lambda^2}\right)

두 개의 기준 파장(예를 들어 프라운호퍼 선의 F'선(청색)과 C'선(적색))에서의 굴절률 차이를 '''평균 분산''' 또는 '''주 분산'''이라고 하며, 다른 두 파장의 굴절률 차이는 '''부분 분산'''이라고 한다. 부분 분산을 주 분산으로 나눈 값을 '''부분 분산비'''라고 한다. 일반적인 광학 유리는 아베 수를 가로축에, 부분 분산비를 세로축에 놓은 그래프에서 어떤 직선 위에 놓이는 성질이 있으며, 이를 '''정상 부분 분산'''이라고 한다. 이에 반해 직선 위에 놓이지 않는 것을 '''비정상 부분 분산'''이라고 한다( '''비정상 분산성''' 또는 '''비정상 분산'''이라고도 함). 선형 응답 이론에서 주파수 응답 함수의 실수부의 변화를 '''분산''', 허수부의 변화를 '''흡수'''라고 한다. 실수부와 허수부 사이에는 크라머스-크로니히 관계식이 성립한다.

5. 2. 도파관 분산

도파관에서는 파의 위상 속도가 구조의 기하학적 형상 때문에 주파수에 따라 달라지는 *도파관 분산* 현상이 나타난다. 일반적으로 파가 특정 영역에 국한되는지 여부에 관계없이, 임의의 불균질 구조(예: 포토닉 결정)를 통해 전파되는 파에 대해 도파관 분산이 발생할 수 있다. 도파관에서는 두 가지 유형의 분산(재료 분산, 도파관 분산)이 일반적으로 나타나지만, 단순히 더해지는 것은 아니다.^[5] 예를 들어 광섬유에서 재료 분산과 도파관 분산은 서로 상쇄되어 영분산 파장을 생성할 수 있으며, 이는 고속 광섬유 통신에 중요하다.

도파관은 재료 구성뿐 아니라 기하학적 구조 때문에 매우 높은 분산성을 갖는다. 광섬유는 현대 통신 시스템에서 널리 사용되는 광학 주파수(빛)에 대한 일종의 도파관이다. 단일 광섬유로 전송할 수 있는 데이터 전송 속도는 다른 현상들 중에서도 색 분산으로 인한 펄스 확산에 의해 제한된다.

일반적으로 전파 상수 β에서 각진동수 ω(β)를 갖는 도파관 모드의 경우(전파 방향 z에서 전자기장이 e^i(βz−ωt)에 비례하여 진동함), 군 속도 분산 매개변수 D는 다음과 같이 정의된다.^[5]

:

D = -\frac{2\pi c}{\lambda^2} \frac{d^2 \beta}{d\omega^2} = \frac{2\pi c}{v_g^2 \lambda^2} \frac{dv_g}{d\omega},

여기서 λ = 2πc/ω는 진공 파장이고, v_g = dω/dβ는 군 속도이다. 이 공식은 균질 매질에 대한 공식을 일반화한 것이며, 도파관 분산과 재료 분산을 모두 포함한다. 이러한 방식으로 분산을 정의하는 이유는 |D|가 단위 거리당 단위 대역폭 Δλ당 (점근적인) 시간 펄스 확산 Δt를 나타내며, 광섬유의 경우 일반적으로 ps/(nm⋅km) 단위로 보고되기 때문이다.

다모드 광섬유의 경우, 소위 모드 분산도 펄스 확산을 일으킨다. 단일 모드 광섬유에서도 두 가지 편광 모드가 존재하기 때문에 편광 모드 분산으로 인해 펄스 확산이 발생할 수 있다. 이들은 전파되는 펄스의 파장이나 대역폭에 의존하지 않으므로 색 분산의 예가 아니다.

5. 3. 광섬유 통신과 분산

광섬유는 현대 통신 시스템에서 널리 사용되는 빛에 대한 일종의 도파관이다. 광섬유에서 재료 분산과 도파관 분산은 서로 상쇄되어 영분산 파장을 생성할 수 있으며, 이는 고속 광섬유 통신에 중요하다.^[5] 단일 광섬유로 전송할 수 있는 데이터 전송 속도는 색 분산으로 인한 펄스 확산에 의해 제한된다.

일반적으로 전파 상수 β에서 각진동수 ω(β)를 갖는 도파관 모드의 경우, 군 속도 분산 매개변수 D는 다음과 같이 정의된다.

:

D = -\frac{2\pi c}{\lambda^2} \frac{d^2 \beta}{d\omega^2} = \frac{2\pi c}{v_g^2 \lambda^2} \frac{dv_g}{d\omega},

여기서 λ = 2πc/ω는 진공 파장이고, v_g = dω/dβ는 군 속도이다. 이 공식은 도파관 분산과 재료 분산을 모두 포함한다. |D|는 단위 거리당 단위 대역폭 Δλ당 시간 펄스 확산 Δt를 나타내며, 광섬유의 경우 일반적으로 ps/(nm⋅km) 단위로 보고된다.

다모드 광섬유의 경우, 모드 분산도 펄스 확산을 일으킨다. 단일 모드 광섬유에서도 편광 모드 분산으로 인해 펄스 확산이 발생할 수 있는데, 이는 색 분산의 예가 아니다.

6. 분산 제어

군분산(GVD)은 펄스의 시간적 확산을 일으켜 광통신 시스템 및 레이저 기술에서 분산 관리를 중요하게 만든다.

광통신에서는 분산이 너무 크면 펄스 그룹이 퍼져 신호를 알아볼 수 없게 되므로 광섬유 길이에 제한을 받는다. 이를 해결하기 위해 군분산이 0인 파장에서 신호를 보내거나, 솔리톤 펄스를 사용하거나, 분산 보상 등의 방법을 쓴다.

레이저에서는 광 공진기의 분산이 펄스 지속 시간을 결정한다. 프리즘 쌍, 회절격자, 차이르드 미러 등으로 분산을 제어한다.

6. 1. 광통신에서의 분산 제어

군분산(GVD)은, 음수이든 양수이든, 궁극적으로 펄스의 시간적 확산을 일으킨다. 이는 광섬유 기반 광통신 시스템에서 분산 관리를 매우 중요하게 만든다. 분산이 너무 크면 비트 스트림을 나타내는 펄스 그룹이 시간적으로 퍼져서 합쳐지므로 비트 스트림을 알아볼 수 없게 된다. 이는 신호를 재생성하지 않고 전송할 수 있는 섬유의 길이를 제한한다.

이 문제에 대한 한 가지 가능한 해결책은 군분산이 0인 파장(예: 실리카 섬유에서 약 1.3~1.5 μm)에서 광섬유로 신호를 보내는 것이다. 이 파장의 펄스는 분산으로 인한 확산이 최소화된다. 그러나 실제로는 군분산이 0이 되면 사파믹싱과 같은 다른 비선형 효과가 증폭되어 더 많은 문제를 야기한다.

또 다른 가능한 방법은 음의 분산 영역에서 솔리톤 펄스를 사용하는 것이다. 이는 비선형 광학적 효과를 이용하여 모양을 스스로 유지하는 광 펄스의 한 형태이다. 그러나 솔리톤은 비선형 효과가 적절한 강도를 가지려면 펄스에서 특정 전력 수준을 유지해야 하는 실질적인 문제가 있다.

현재 실제로 사용되는 해결책은 분산 보상이다. 이는 일반적으로 분산 효과가 상쇄되도록 반대 부호의 분산을 가진 다른 섬유와 섬유를 매칭하는 방식이다. 이러한 보상은 자기위상변조와 같은 비선형 효과에 의해 제한되는데, 이는 분산과 상호 작용하여 분산을 되돌리는 것을 매우 어렵게 만든다.

6. 2. 레이저에서의 분산 제어

초단 펄스를 생성하는 레이저에서도 분산 제어가 중요하다. 광 공진기의 전반적인 분산은 레이저가 방출하는 펄스의 지속 시간을 결정하는 주요 요소이다. 프리즘 한 쌍을 사용하여 순 음의 분산을 생성할 수 있으며, 이는 일반적으로 양의 분산을 갖는 레이저 매질의 균형을 맞추는 데 사용할 수 있다. 회절격자를 사용하여 분산 효과를 생성할 수도 있는데, 이는 종종 고출력 레이저 증폭 시스템에 사용된다. 최근에는 프리즘과 격자의 대안으로 차이르드 미러가 개발되었다. 이러한 유전체 미러는 서로 다른 파장이 서로 다른 침투 길이를 가지고 따라서 서로 다른 군 지연을 갖도록 코팅되어 있다. 코팅층은 순 음의 분산을 달성하도록 조정할 수 있다.

7. 정상 분산과 이상 분산

파장이 짧아질수록 굴절률이 증가하는 경우를 '''정상 분산'''(normal dispersion^영어)이라고 한다. 가시광선 영역에서 투명한 물질은 가시광선 영역에서 정상 분산이 일어난다. 가시광선 이외에도 물질의 공명 파장에서 벗어난 영역에서는 정상 분산이 일어난다. 일반적으로 굴절률이 높은 물질일수록 정상 분산이 더 크다.

이와 반대로, 공명 파장 부근에서는 굴절률이 감소하고, 장파장광이 단파장광보다 크게 굴절한다. 이것을 '''이상 분산'''(anomalous dispersion^영어)이라고 한다.

공명 파장 및 그 근방 이외의 굴절률은 셀마이어의 분산 공식으로 나타낼 수 있다.

: $n^2 = n_\infty^2 + {A' \over \lambda^2 - {\lambda_A}^2} + {B' \over \lambda^2 - {\lambda_B}^2} + \dots$

'''A′''', '''B′''', ... 및 '''λ''', '''λ''', ...는 물질에 따라 다른 매개변수이다. '''λ''', '''λ''', ...는 공명 파장이며, 즉 ('''n'''² 이외의) 항은 공명 파장의 수만큼 존재한다.

이것을 $\lambda$ 에 대해 급수 전개하면 다음 식이 된다.

: $n^2 = A + {B\over \lambda^2} + {C\over \lambda^4} + \cdots - B' \lambda^2 - C' \lambda^4 - \cdots$

셀마이어의 분산 공식은 공명 파장에서는 발산한다. 그러나 그 근방 이외에서는 정상 분산과 이상 분산에 대해 좋은 일치를 보인다. 흡수도 고려한 식은 헬름홀츠에 의해 제시되었다.

밀도가 높은 매질에서는 적외선 영역에 있는 이온 공명 파장을 고려한 셀마이어의 분산 공식이 사용된다.

일반적으로 투명한 매질은 절연체(유전체)이다(도체라면 에너지가 줄열로 흡수된다). 이때 매질 속 분자가 전자파의 전기장에 의해 분극되는 전기쌍극자 모델로 근사할 수 있지만, 공명파장이 자외선 영역에 있으므로 기체와 같은 밀도가 낮은 매질(굴절률 $n \approx 1$ )에서는 가시광선 영역에서 다음 식으로 근사할 수 있는 것으로 알려져 있다(오귀스탱 루이 코시(Augustin-Louis Cauchy)에 의해 경험적으로 구해졌으므로 코시의 분산 공식이라고 한다). 다음에서 A, B, C 등은 측정에 의해 결정되는 상수이다.

: $n - 1 = A \left( 1 + {B \over \lambda^2}\right)$

코시의 분산 공식은 셀마이어의 분산 공식의 근사 형태이다.

이상의 분산 공식 외에도 다음과 같은 식이 제안되었다.^[15]

: $n^2 = \frac{\mu_r \epsilon_r}{2} \left(\sqrt{1+\left(\frac{\sigma}{\epsilon}\frac{\lambda}{2\pi c}\right)^2}+1\right)$

여기서 μ_r은 비투자율, ε_r은 비유전율, σ는 도전율, ε은 유전율이다.

두 개의 기준 파장(예를 들어 프라운호퍼 선의 F'선(청색)과 C'선(적색))에서의 굴절률 차이를 '''평균 분산''' 또는 '''주 분산'''이라고 하며, 다른 두 파장의 굴절률 차이는 '''부분 분산'''이라고 한다. 부분 분산을 주 분산으로 나눈 값을 '''부분 분산비'''라고 한다. 일반적인 광학 유리는 아베 수를 가로축에, 부분 분산비를 세로축에 놓은 그래프에서 어떤 직선 위에 놓이는 성질이 있으며, 이를 '''정상 부분 분산'''이라고 한다. 이에 반해 직선 위에 놓이지 않는 것을 '''비정상 부분 분산'''이라고 한다( '''비정상 분산성''' 또는 '''비정상 분산'''이라고도 함).

8. 펄서 방출과 분산

펄서는 밀리초에서 수 초에 이르는 매우 규칙적인 간격으로 펄스를 방출하는 회전하는 중성자별이다. 천문학자들은 이 펄스가 넓은 주파수 범위에 걸쳐 동시에 방출된다고 믿는다. 그러나 지구에서 관측했을 때, 더 높은 무선 주파수에서 방출된 각 펄스의 구성 요소는 더 낮은 주파수에서 방출된 것보다 먼저 도착한다. 이러한 분산은 성간 매질의 이온화된 성분(주로 자유 전자) 때문에 발생하며, 이로 인해 군 속도가 주파수에 따라 달라진다. 주파수 ν|뉴^영어에서 추가되는 지연 시간은 다음과 같다.^[12]

: $t = k_\text{DM} \cdot \left(\frac{\text{DM}}{\nu^2}\right),$

여기서 분산 상수 ''k''_DM은 다음과 같이 주어진다.

: $k_\text{DM} = \frac{e^2}{2 \pi m_\text{e} c} \approx 4.149~\text{GHz}^2\,\text{pc}^{-1}\,\text{cm}^3\,\text{ms},$

'''분산 측정값'''(DM)은 자유 전자의 기둥 밀도(전체 전자 수) 즉, 펄서에서 지구까지 광자가 이동한 경로를 따라 적분된 전자의 수 밀도 ''n''_e이며 다음과 같이 주어진다.

: $\text{DM} = \int_0^d n_e\,dl$

단위는 입방 센티미터당 파섹(1 pc/cm³ = 30.857Gm²)이다.^[13]

일반적으로 천문 관측의 경우 방출 시간을 알 수 없기 때문에 이 지연 시간을 직접 측정할 수 없다. 측정할 수 있는 것은 두 가지 다른 주파수에서 도착 시간의 차이이다. 고주파수 ν|뉴^영어_hi와 저주파수 ν|뉴^영어_lo 펄스 구성 요소 사이의 지연 Δ''t''는 다음과 같다.

: $\Delta t = k_\text{DM} \cdot \text{DM} \cdot \left( \frac{1}{\nu_\text{lo}^2} - \frac{1}{\nu_\text{hi}^2} \right).$

위의 방정식을 Δ''t''로 다시 쓰면 여러 주파수에서 펄스 도착 시간을 측정하여 DM을 결정할 수 있다. 이것은 다시 성간 매질을 연구하는 데 사용될 수 있으며, 서로 다른 주파수에서 펄서를 관측하는 것을 결합할 수 있게 해준다.

한국의 천문학 연구에서는 펄서 신호의 분산 현상을 이용하여 우주 공간의 전자 밀도 분포를 연구하고, 이를 통해 우주의 구조와 진화를 이해하는 데 기여하고 있다.

9. 보석학에서의 분산

보석학에서 분산은 보석의 광채("fire")를 결정하는 중요한 요소이다. 분산은 B와 G (각각 686.7 nm와 430.8 nm) 또는 C와 F (각각 656.3 nm과 486.1 nm) 프라운호퍼 파장에서 측정한 물질의 굴절률 차이로 정의된다.^[10] 보석의 광채는 분산의 정도, 면각, 연마 품질, 조명, 굴절률, 색상 채도, 관찰 방향 등에 따라 달라진다.^[10]^[11]

다음은 다양한 보석의 분산 값(B와 G 프라운호퍼 파장에서 측정한 굴절률 차이)을 나타낸 표이다.^[10]

광물의 분산 값
광물 이름	분산 값 ()
적철광	0.500
진사 (HgS)	0.40
합성 루틸	0.330
루틸 (TiO₂)	0.280
아나타제 (TiO₂)	0.213–0.259
불석	0.203
바나진석	0.202
파불라이트	0.190
섬아연석 (ZnS)	0.156
황 (S)	0.155
안티몬탄탈라이트	0.146
수침철석 (FeO(OH))	0.14
브루카이트 (TiO₂)	0.131
리노베이트	0.13
홍아연석 (ZnO)	0.127
합성 모이사나이트 (SiC)	0.104
석영석 (SnO₂)	0.071
지르코니아 (ZrO₂)	0.060
파웰라이트 (CaMoO₄)	0.058
안드라다이트	0.057
데만토이드	0.057
능철석	0.055
타이타나이트	0.051
베니토이트	0.046
청연석	0.044
다이아몬드 (C)	0.044
합성 석영석 (SnO₂)	0.041
플린트 유리	0.041
히아신스	0.039
자르곤	0.039
스타라이트	0.039
휘석	0.038
지르콘 (ZrSiO₄)	0.039
GGG	0.038
디옵타스	0.036
휘비나이트	0.034
석고	0.033
설화석고	0.033
에피도트	0.03
탄자나이트	0.030
툴라이트	0.03
조이사이트	0.03
YAG	0.028
스페사틴	0.027
우바로바이트	0.027
알만딘	0.027
헤소나이트	0.027
윌레마이트	0.027
플레오나스트	0.026
로돌라이트	0.026
붕소석	0.024
빙정석	0.024
십자석	0.023
피로프	0.022
다이아스포어	0.02
그로슐라	0.020
헤미모르파이트	0.020
규선석	0.020
감람석	0.020
스피넬	0.020
베수비아나이트	0.019–0.025
가닛	0.019–0.021
클리노조이사이트	0.019
래브라도라이트	0.019
액시나이트	0.018–0.020
디옵사이드	0.018–0.020
에카나이트	0.018
강옥 (Al₂O₃)	0.018
합성 강옥	0.018
루비 (Al₂O₃)	0.018
사파이어 (Al₂O₃)	0.018
코르네루핀	0.018
신할라이트	0.018
소달라이트	0.018
로도자이트	0.018
히든나이트	0.017
쿤차이트	0.017
스포듀민	0.017
전기석	0.017
감람석	0.017
단부라이트	0.017
헤르데라이트	0.017
루벨라이트	0.017
아크로이트	0.017
드라바이트	0.017
엘바이트	0.017
인디콜라이트	0.017
리디코아타이트	0.017
회장석	0.017
슈롤	0.017
베르데라이트	0.017
남정석	0.016
중정석 (BaSO₄)	0.016
유클라스	0.016
데이톨라이트	0.016
알렉산드라이트	0.015
크리소베릴	0.015
콘드로다이트	0.015
실리마나이트	0.015
함버거이트	0.015
피록스망가나이트	0.015
합성 휘석	0.015
스미소나이트	0.014–0.031
암블리고나이트	0.014–0.015
아쿠아마린	0.014
녹주석	0.014
에메랄드	0.014
헬리오도어	0.014
모가나이트	0.014
브라질리아이트	0.014
셀레스타이트	0.014
토파즈	0.014
고셰나이트	0.014
인회석	0.013
아벤츄린	0.013
자수정 (SiO₂)	0.013
시트린	0.013
프라시오라이트	0.013
석영 (SiO₂)	0.013
장미석영 (SiO₂)	0.013
연수정 (SiO₂)	0.013
무수석고	0.013
돌로마이트	0.013
모리온	0.013
장석	0.012
문스톤	0.012
정장석	0.012
폴루사이트	0.012
조장석	0.012
회장석	0.012
합성 에메랄드	0.012
마그네사이트 (MgCO₃)	0.012
사장석	0.012
선스톤	0.012
합성 알렉산드라이트	0.011
합성 사파이어 (Al₂O₃)	0.011
인산철광	0.010–0.011
페나카이트	0.01
캔크리나이트	0.010
류사이트	0.010
사방휘석	0.010
흑요석	0.010
사장석	0.009–0.010
양기석	0.009
제레메제바이트	0.009
네펠린	0.008–0.009
방해석	0.008
하우인	0.008
나트롤라이트	0.008
합성 석영 (SiO₂)	0.008
아라고나이트	0.007–0.012
오제라이트	0.007
베릴로나이트	0.010
스트론티아나이트	0.008–0.028
방해석 (CaCO₃)	0.008–0.017
형석 (CaF₂)	0.007
트레몰라이트	0.006–0.007

참조

_[1] 서적 Principles of Optics https://archive.org/[...] Cambridge University Press 1999-10-00
_[2] 웹사이트 Dispersion Compensation http://www.proximion[...] 2015-08-25
_[3] 웹사이트 Calculation of the Mean Dispersion of Glasses http://glassproperti[...]
_[4] 서적 Principles of Optics Pergamon Press 1980
_[5] 서적 Optical Networks: A Practical Perspective Academic Press 1998
_[6] 웹사이트 Chromatic Dispersion http://www.rp-photon[...] Wiley 2008
_[7] 학술지 Prismatic discontinuous Galerkin time domain method with an integrated generalized dispersion model for efficient optical metasurface analysis 2020-10-01
_[8] 서적 Electrodynamics of Continuous Media Butterworth-Heinemann 1984
_[9] 학술지 Taming spatial dispersion in wire metamaterial 2008-07-01
_[10] 서적 Gemstones of the World https://books.google[...] Sterling Publishing Company 2011-12-31
_[11] 웹사이트 What is gemstone dispersion? http://www.gemsociet[...] 2015-03-09
_[12] 간행물 Single-Dish Radio Astronomy: Techniques and Applications Astronomical Society of the Pacific 2002
_[13] 서적 Handbook of Pulsar Astronomy Cambridge University Press 2005
_[14] 서적 学術用語集分光学編 http://sciterm.nii.a[...] 培風館 1999
_[15] 서적 エアロゾル学の基礎森北出版 2003

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com